Movimiento Circular y Movimiento Armónico simple

para encontrar la ecuación de posición de un movimiento armónico simple es necesario aplicar la semejanza , con el movimiento circular

En esta gráfica podemos observar diversas situaciones . una de ellas , es que cada grado de la circunferencia representa un punto del desplazamiento oscilatorio osea las posiciones que sigue el movimiento armónico simple  , en donde el centro del circulo seria el punto de equilibrio , 90 grados la posición mínima y 180 la máxima, y finalmente al unir cada punto de la circunferencia nos daremos cuenta que forma una razón trigonométrica , la cual puede variar entre Seno y Coseno , en el caso del ejemplo la razón trigonométrica representada es Seno      

Entonces la formula posición máxima  es la siguiente (esta formula se aplica cuando el objeto que esta oscilando se encuentra en el máximo punto de elongación   :   X= A cos (WxT)  

• Posición mínima , quiere decir lo máximo que se puede reducir en el movimiento oscilatorio 
• En donde X es posición
• A es la amplitud , ya que hablamos de los puntos mínimos y máximos del movimiento M.A.S
• Cos , representa la rozan trigonométrica faltan te , ya que si  el movimiento oscilatoria esta alrededor de un circunferencia siempre representa a Seno 
• W representa la velocidad angular  , ya que es necesario saber con que velocidad se desplaza de un punto a otro 
• T representa el tiempo , indicando cuanto tarde en pasar por cierto punto del movimiento oscilatorio 

formula de posición normal , esta se utiliza cuando el objeto que esta oscilando se encentra en cualquier otra posición que no sea la máxima : X = A cos (WxT +  O  )

• Las razones son las mismas que las anteriores , lo único que varia es que se le añade el angulo , el cual representa la elongación que recorrió en cierto momento de la oscilación que , cabe recordar , que la X es también una elongación ( posición ) , la diferencia es que es la elongación que se quiere a llar  o encontrar en cierto momento de la oscilación

Ejercicio 

Un objeto posee un movimiento circular con periodo de 0,1s , y un radio de 5cm calcule 

• La velocidad Angular del movimiento 
• La ecuación de posición del objeto 
• y a lle donde se encuentra a los 0,25s 

a) Formula a utilizar :  W =  O  =  2II rad    =  62,83 rad/s  (Velocidad Angular ) 

                                              T         0.1s

esta es una de las formulas que se pueden utilizar para a llar la velocidad angular , mas adelante veremos otra mas ; Ademas lo que sucedió en ella fue que el ejercicio nos plantea que es un movimiento circular , es decir al dar una vuelta recorre 360° ¿no?  , y al pasarlo a unidades de rad equivale a 2II rad ,dejando en claro por que se utilizo este valor , y el T equivale a el periodo que realiza este movimiento circular , el cual ya nos dan el dato y es 0,1s  

b)    A= 5cm = 0,05M ( Converción )        X =  0,05M cos ( 62,83rad/s x t ) 

                                                                    X=  0,05M cos (62,83rad/s x 0,23s )

                                                                    X=  0,05M cos (14.4509 )

                                                                    X= 0,05M ( -0.3086)

                                                                              R/ X= -0.01543 

En este caso para a llar la posición que nos pedían utilizamos la formula de máxima posición  ya que a un que en el texto del ejercicio  no lo mencionen , para empezar el movimiento , tiene que empezar en la posición máxima , por esta razón se utilizo X= A cos ( W x t )

Ejercicio (2 )

El angulo de desface del movimiento armónico simple si se tienen las siguientes condiciones 

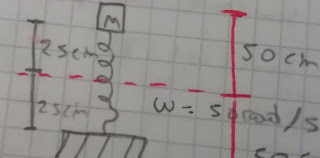
• Amplitud = 50cm              (Conversión)   0,5M  
• Posición actual = 0.25M
• W= 50 rad/s
•  t = 2s 

(Si se quiere representar gráficamente , su representación seria la siguiente )

(intenten analizar la  )

a)   Cabe aclarar que el objetivo en este ejercicio es el siguiente  O y para lograr eso podemos implementar la siguiente formula  X= A cos (W x t + O )ya que estamos buscando el angulo de desface , ya que la posición actual ya nos la dan , la cual es X = 0,25M  , justo con todos los demás datos de la formula , cabe resaltar que es necesario que solo aya una incógnita y nunca 2 

                                                     X= A cos ( W x t + O )

                                                 0,25= 0,5 cos ( 50 x 2 + O)

                                                 0,25=cos (100+O )

                                                  0,5

                                Aquí pasamos a dividir el 0,5 y resolvemos la división  

                                                  Cos-1 (0.5) = 100 +O 

        Cancelamos el coseno con un Cos-1 , pero este no se quita si no que le saca el Cos-1 al (0,5) 

                                                 1.04= 100 + O

                                                 1.04-100 = O

         Pasamos el 100 a restar y tenemos como resultado el angulo de desface 

                                                              

                                                                  R/  -98.95rad = O

No esta de menos mencionar  , que se puede utilizar este método para encontrar cualquier incógnita que este en la ecuación , por ultimo , hay un truco mas en el caso del movimiento circular y el movimiento armónico simple ,el cual es : 

Que se puede remplazar el tiempo por 0 para determinar de adonde empieza el movimiento oscilatorio :

                                                 X= 0,5 cos ( 50 x 0 -98.96 ) 

                                                 X= 0,5 cos ( -98.96 )

                                                 X= 0,5 cos [ - 1,6 x -0,00010 )

                                                 X= -0,000084 M 

Para finalizar el tema , no olviden que siempre hay que colocar las unidades con ka  cual finaliza  la ecuación , como en este caso fue , metros; Ahora finalmente les dejaremos algunas ecuaciones que pueden llegar a implementar  en el realiza-miento de un ejercicio  :

Velocidad = Ecuación M.A.S 

V= -(W) A sen ( W x t ) ------------> Punto Máximo

V= -(W) A sen ( W x t + O ) -------> Ecuación General  

Vmax= W x A -----------------------> Velocidad máxima que se puede alcanzar 

Aceleración = Ecuación M.A.S 

a= -(W)2 x A cos ( W x t ) -----------> Punto Máximo ;(2) es elevado a la dos  

a= -(W)2 x A cos ( W x t + O ) ------> Ecuación General 

a max = -(W)2 x A --------------------> Aceleración Máxima que se puede alcanzar 

 Velocidad Angular y Periodo  = Ecuación

W= 2II    

         T              

W = ( Raíz cuadrada  )  K

                                      m --------> Masa 

T = 2II x ( Raíz cuadrada ) m

                                            K